又是很久没写东西了,大半年?差不多吧。久了不写都不知道该写什么了。
6月的时候写了个小demo,有人想问原理或者说怎么实现的,但是一直懒得理。鉴于这个小程序并不是几千行的冗长代码,所以今天简单解释一下吧,希望可以勾起一些人的兴趣。
大家从大一进校开始就被很多人鼓吹数学无用论,所以,这里偏要讲一下如何用数学知识来编程。神马数据结构、操作系统、计算机网络都不需要,你需要的只是数学以及对编程语言的一点点了解。
要讲的demo为一个小球无阻尼运动下与直线碰撞并无能量损失地反弹的小例子。如图:

绿色部分为小球运动轨迹,白色为直线。你可以理解为入射光线在某平面发生镜面反射。
那么,开始吧!
如果实现语言为C++的话,那么这个小球很明显应该封装成为一个类,如果用C语言,那就用函数慢慢磨吧,效果一样。
平面物体运动轨迹的参数方程大致为:
![]() (话外音: kao,搞得这么神神叨叨的…说白了就一曲线方程嘛)
(话外音: kao,搞得这么神神叨叨的…说白了就一曲线方程嘛)
但是如果程序模拟的话就不用这么麻烦。 (废话,这不白写了)
咱们一般用的 △x 和 △y 每一帧让x和y自加,这样就得到了x和y的下一个位置,如此迭代,那物体自然运动起来啦~ 至于△x和△y的值,则有
![]()
假如方程为一次线性方程的话,![]() 和
和 ![]() 就与 t 无关了,所得到的△x 和 △y就是一个确定的数。如果
就与 t 无关了,所得到的△x 和 △y就是一个确定的数。如果![]() 和
和 ![]() 中的任何一个依然含有参数t的话,则需要再次求导,直到不含有t为止。可以理解为物理上的变加速直线运动,加速度自身也有N次加速度。如果非线性方程,则需要其他解决方案,这里不讨论。
中的任何一个依然含有参数t的话,则需要再次求导,直到不含有t为止。可以理解为物理上的变加速直线运动,加速度自身也有N次加速度。如果非线性方程,则需要其他解决方案,这里不讨论。
我们知道,一个质点只有速度质量,没有体积或者面积的概念,所以无法进行碰撞检测,还需要给小球加入一个半径。(由于在2D上讲,所以“小球”所指代的仅仅为一个“圆形”,为方便描述,把它叫做小球)
而本次仅描述匀速直线运动,所以小球需要的参数为: (先使用伪代码描述)
Ball:
{
float x, y; //小球当前相对于屏幕的位置
float dx,dy; //小球的 △x 和 △y
float radius; //小球半径
COLOR color; //为便于区分,可以给小球加一个随机的RGB颜色属性
}
如此,小球构造完毕。
接下来是直线。我们知道,两点定线。只要给你两个点的坐标P(x0, y0),Q(x1, y1),你就能把直线PQ方程算出来。
先求得直线的斜率
k = tanθ = (y1-y0) / (x1-x0) (θ为直线倾斜角,后面计算反射角要用到)
联立二元一次方程组
![]()
将上面的k 带入方程组,解得直线方程为:
( 以 Ax + By + C = 0 形式给出如下 )
(y0 – y1)x + (x0 – x1)y + (x0*y1 – x1*y0)
= 0
( 此时系数有 A = y0 – y1, B = x0 –
x1, C = x0*y1 – x1*y0 )
若要化为 y = kx + b 的形式,则需注意(x0 – x1) 的值,如果所得直线为一条垂线的话,则x0 – x1 = 0 , 那么 无法得到 y = kx + b 形式。 而通常这种形式便于计算,所以我们设计时考虑清楚就行了。
当直线不为垂线时,可得: (以下为 y = kx +
b 形式)
y = [(y0 – y1)/(x0-x1)]x + [(x0*y1 –
x1*y0) /(x0-x1)]
( 此时若按照Ax + By + C = 0 形式系数有 A = (y0 – y1)/(x0-x1), C =
(x0*y1 – x1*y0) /(x0-x1), B = -1 )
当直线为垂线时,反射角非常容易计算,直接将小球的x方向的速度取反即可,可以直接实现。(当直线为水平线时,反射角也非常容易计算,通常直接将y方向的速度取反。)
所以线段所需要的参数为: (数学上的直线是无限长的,而屏幕上所用的均为线段)
Line:
{
int x0, y0; //线段端点 P
int x1, y1; //线段端点 Q
int a, b, c; // a = A,
b = B, c = C, 其中 A、B、C即为上面所求出的系数
}
现在,我们就可以根据直线方程和小球坐标、小球半径计算出小球是否碰到直线,如果碰到,并进行反射了。
这里总共需要三步。
第一,我们必须计算出小球到直线的距离,假如小球到直线的距离大于小球的半径,那么小球肯定不可能与直线相撞。这也是为什么小球必须有一个半径的原因。而这个半径也必须选择合适,因为我们是按帧模拟,假如小球速度过快(即△x或△y过大),上一帧在直线一头很远的位置,下一帧加上△x和△y以后跑到直线另一端很远的位置去了,这样是检测不到的。 而假如没处理好,跑到某个不能到达的位置,则可能卡在里面再也出不来。一些网游就有这种毛病,人物卡在地图某个地方,特别蛋疼。
第二,如果小球与直线的距离小于等于小球半径,这样也不一定与线段相撞,因为有可能是如下情况:

要知道,直线是无限长的,而线段是有限长的,我们计算的点到直线的距离是以直线为基准,但并不表示小球就能碰上该线段。
这一步需要计算小球到直线的投影坐标,并且确定这个投影坐标是否在直线内。(PS:这个投影坐标可以抽象地理解为过小球做直线AB垂直于我们的直线PQ,交于点O, 点O坐标即为这个投影坐标。如果点O在线段PQ上,且小球到直线距离小于等于直线半径,则小球与直线相撞)
第三, 如果确定小球与直线相撞,我们需要根据小球的运动公式与直线方程求出小球的反射角或者说反射方向。进一步将小球反射出去。如果有能量抵消,阻力、引力等因素,这一步的处理会更加复杂,篇幅有限,咱不考虑。
下面,跟着我一步一步求出这些吧!
第一步,求距离:
这个很简单,大家都会,一个点 (x0, y0) 到 直线 Ax + By + C
= 0 的距离有:
距离 ![]()
其中x0, y0 即为待测小球当前位置,A,B,C即为前面求得的直线方程系数,代入即可。
第二步,求投影坐标:
这一步稍麻烦,需要拿纸笔算一下。
根据前面的直线方程 y = kx + b (前面已经讨论过 Ax + By + C = 0 与之转化的问题,可自行回顾) 中,斜率为k可知, 直线的垂线斜率k’有
k * k’ = -1 è k’ = -1/k
在这里,如果直线为水平线,则存在 k = 0 的问题,需要单独考虑。
由直线垂线过小球坐标点(x0, y0) 可得:
y – y0 = k’(x – x0)
其中,将k’ 一步一步换为已知的直线参数A,B,C表示,则得到一个可用的方程。
再联立方程组
![]()
接下来需要对方程组进行求解。
根据前面已经求得的k和k’,使用克莱默法则构造2*2行列式进行求解。
计算虽然也不是特别复杂,但笔者在纸上完成,所以这里不多阐述。有兴趣的请自备纸笔演算一下。
解得:
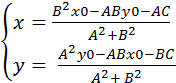 (PS: 用公式编辑器的感觉真不错,虽然放这里看不出来了)
(PS: 用公式编辑器的感觉真不错,虽然放这里看不出来了)
这样就获得了投影坐标(x,y), 若线段两端点为P(x0, y0), Q(x1, y1)
那么,如果解得的 x 在 x0和x1之间并且y在y0和y1之间,小球就与直线真正碰撞了。前面说过,k有可能为0, 所以k’可能不存在,但最终解出来的结果中,分母是有意义的,且与k’本身无关。所以该种代换以及中间步骤的变换,在这里可以忽略。
第三步 反射小球
最后一步了,这一步相对比较麻烦。因为大家在电脑上一般使用的屏幕坐标系,与我们平时数学演算使用的笛卡尔坐标系这样的有区别,那就是屏幕坐标系中y轴值是自上往下递增的。当然,不少图形库的实现遵从了数学上的坐标系,如OpenGL等,但这种小玩意就不劳驾它老人家了,咱直接用屏幕坐标系画出来。这样就涉及到一些反向的转换,需要特别注意。
反射小球时,需要先测量小球的入射方向。(你也可以用其他更好更复杂方法,我是这样用的,所以只讨论这种方法)
这个方法比较简单,只要注意好y轴的方向,就可以轻易求出,不过笔者还是在这里蛋疼老了半天才做好。
你可以用反正余弦或者反正余切求出,但必须必须估算好求反正余弦反正余切函数的定义域和值域。
首先,函数中传入小球运动的方向向量,这里用 △x 和 △y代替。(该计算起来跟直接的(x, y) 这样的向量垂直,但如果直线也按此种方式的话,就不影响结果,方便运算)
接下来任选一种方式,如反正弦方式:
可以直接求得
![]()
反正弦方式还好,假如用反正余切的话,必须注意分母可能为0的情况。为了安全,反正余弦也可以注意一下。
而到这里也别高兴得太早,前面说过,要注意值域问题,arcsin 的值域为[-π/2,π/2]
而小球的反射方向是[0, 2π],所以我们必须对所得的Angle应对于arcsin函数的值域进行转换,
在平面上,[-π/2, 0] 的角与[3π/2, 2π] 的角产生的方向是相同的 (这里提到的夹角方向可以这样理解:在坐标系中,一个向量开始为x轴正方向,沿逆时针方向旋转这个夹角的度数之后,向量的方向) ,如果仅仅需要方向的话可不必管它,但这里是计算反射角,所以必须全部加以处理。
如何得到处理过程就不多说,有兴趣可以自行摸索。计入屏幕坐标系所需的转换,需要进行的处理如下:
(1) 如果△x ≥ 0:
①如果△y ≥ 0, 则 Angle 本身即为所求
②如果△y < 0, 则 Angle + 2π 即为所求
(2) 如果△x < 0 则π – Angle 即为所求
到此,获取小球入射方向的方法找到了。(特别注意!! 入射方向 ≠ 入射角, 入射角是入射方向与直线法线之间的锐夹角, 请看下图蓝色标注部分)
接下来需要计算小球出射方向,这里画个图,便于理解
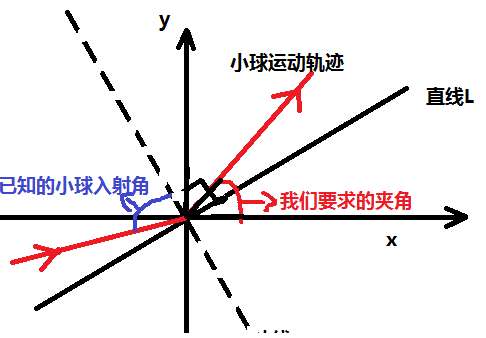
下面给每条线一个标记,然后加以计算。
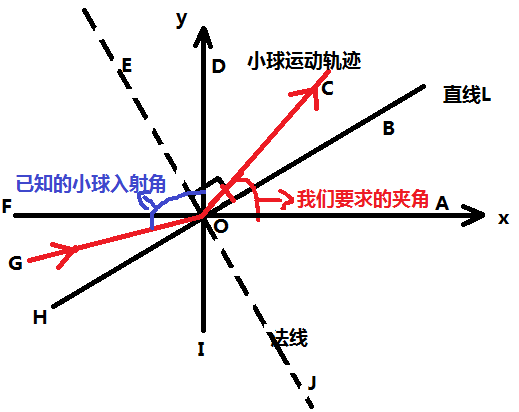
现在我们做的完全变成了一道数学题,小球的入射方向为已知,其中由于直线方程已知,所以∠AOB、∠AOE为可求得的已知,我们需要根据这些已知条件来求∠AOC。
这时,很多人都会被这个图给迷惑,以为小球的方向角就是∠AOG而感觉无从下手。
但是,我们注意下小球入射的方向。而我们的夹角是如何算的?
再看下面的图:
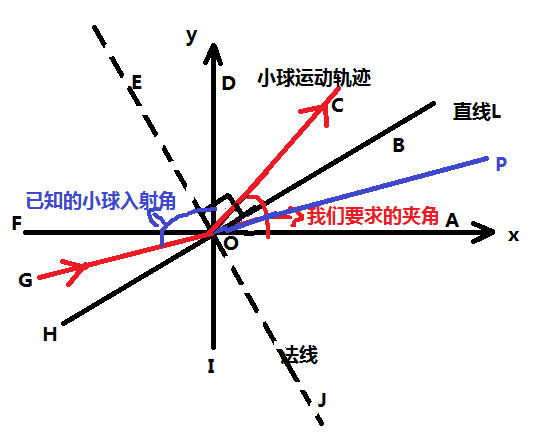
作GO的延长线 OP, 此时 GP为一条直线。此刻我们很清楚地看到,小球的入射方向与x轴的夹角为∠AOP。 而∠AOP 就等于我们上一步求得的方向角”Angle”
通过分析可以得出,∠BOP = ∠BOC
而∠BOP = ∠BOA – ∠POA
所以 ∠AOC = ∠BOA + ∠BOC = 2∠AOB – ∠AOP
而∠AOP已求得,所以现在仅需求得∠AOB,也就是直线L与x轴的夹角。
由于直线方程已知为 Ax + By + C = 0,(或 y = kx + b 形式)
求个偏导可以看出,Adx + Bdy = 0, 所以 (-B, A)或者 (B,
-A) 就相当于前面的(△x, △y)
而在笔者的代码中,使用的y = kx + b 形式,所以使用的向量为 (1, k)
同第三步开始的计算方式相似,可以得到直线与x轴的夹角如下:
![]()
并进行如下转换:
① 如果k ≥ 0, 则![]() 本身即为∠AOB
本身即为∠AOB
② 如果k < 0, 则![]() + 2π 即为∠AOB
+ 2π 即为∠AOB
至此,三步结束,最后得到了∠AOC, 然后根据![]() 可以算出相应的小球反射后的方向,即
可以算出相应的小球反射后的方向,即
△x = speed * cos∠AOC
△y = speed * sin∠AOC
程序编写结束。
点击此处下载程序的C++代码实现以及可执行程序
It抯 awesome for me to have a website, which is useful designed for my know-how. thanks admin wow gold sale http://qaci.eq.edu.au/index.php/member/172769/
啦啦啦